“Menantang Asumsi”
Tujuan berpikir lateral adalah untuk mempermasalahkan setiap asumsi, sebab tujuan dari semua proses berpikirnya adalah untuk menyusun kembali setiap pola. Kesepakatan umum mengenai suatu asumsi tidak selalu menjamin bahwa asumsi itu adalah tepat, sebab kontinuitas historisnyalah (turun-temurun) yang menyatakan kebenarannya, bukan atas dasar penilaian yang berulang untuk memastikan keabsahannya.
Contoh Kasus 1:
Susunlah 3 bentuk benda berikut sehingga menghasilkan 1 visualisasi benda yang mudah dijelaskan!
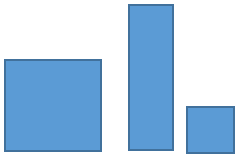
Yang biasa kita lakukan adalah langsung menyusun benda-benda tersebut menjadi satu bentuk tertentu, sehingga tidak jarang kita mengalami kesulitan akan menjadi apa nantinya. Pola pikir lateral akan mengarahkan kita, alih-alih langsung menyusun, melainkan memerika kembali setiap bentuk sehingga ditemukan kemungkinan untuk melakukan “pembelahan” segi empat besar menjadi dua. Dari situ, ditemukanlah sebuah visualisasi pola yang dapat dijelaskan dengan lebih mudah.
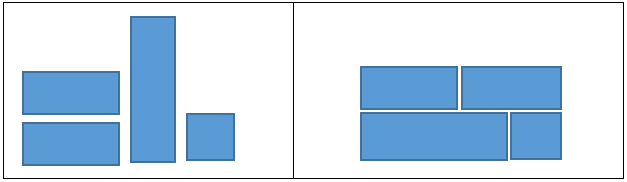
Kecenderungan yang sering terjadi sebagai tanggapan kita adalah “Kan perintahnya diminta untuk menyusun, bukan membelah atau memotong gambar tersebut!” Persis di sinilah yang dimaksud dengan ASUMSI yang tertanam di dalam pemikiran kita bahwa: bentuk yang disajikan tidak dapat diubah.
Contoh tersebut memberikan gambaran kepada kita bahwa suatu masalah ada kalanya tidak dapat dipecahkan hanya dengan menyusun “potongan-potongan” data yang tersedia, tetapi masalah justru dapat dipecahkan dengan memeriksa ulang setiap potongan-potongan tersebut agar dipastikan memiliki informasi yang tepat dalam memecahkan masalahnya.
Dalam proses pemecahan masalah, kita cenderung mengasumsikan batasan-batasan tertentu, tetapi tanpa sadar, batasan-batasan itu justru menempatkan kita pada cara berpikir yang tidak kreatif. Dalam menantang asumsi kita mesti menantang juga batasan, lalu mengarahkan cara berpikir kita untuk menyusun kembali pola-pola yang mungkin.
Contoh Kasus 2:
Menghubungkan sembilan titik dengan hanya menggunakan empat garis lurus yang bersambungan tanpa mengangkat pensil dari kertasnya.
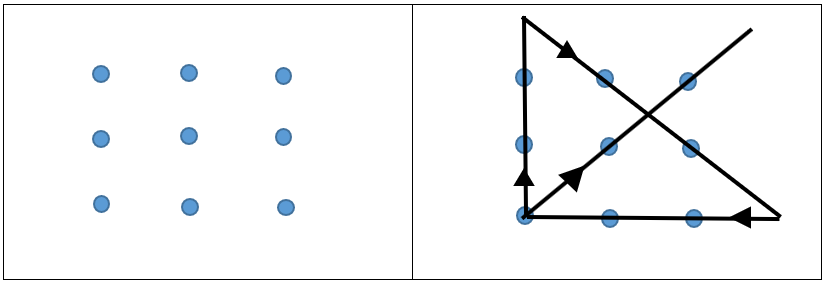
Asumsi yang digunakan dalam menyelesaikan masalah ini adalah bahwa: titik-titik harus menjadi awal dan akhir pergerakan pensil tanpa boleh melebihi batas (sehingga selalu berakhir dengan lebih dari empat garis). Dengan melanggar asumsi tersebut, di mana pensil boleh bergerak di luar batasan titik, maka masalah dapat dipecahkan dengan mudah.