
💠 Grafik membuka ke atas f(x) = ax2 + bx + c


💠 Grafik membuka ke bawah
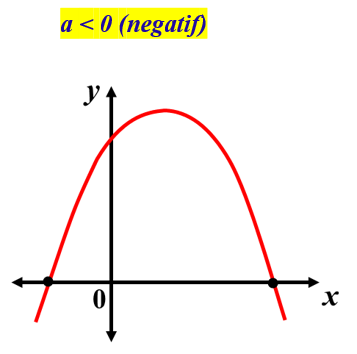



Perhatikan grafik berikut:

Grafik fungsi berpotongan dengan sumbu x di titik (a, 0) dan (b, 0).
Hal ini menunjukkan bahwa untuk x = a dan x = b diperoleh nilai y yang sama, yaitu 0.
Nilai x yang menghasilkan y = 0 disebut pembuat nol fungsi.

Tentukan pembuat nol fungsi dari persamaan y = f(x)= x2 + 2x – 3




Rumus persamaan sumbu simetri:

Perhatikan grafik berikut ini!
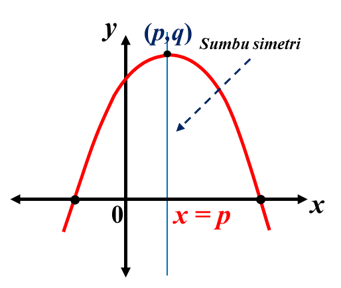
Grafik fungsi di samping simetris terhadap garis vertikal yang melalui (p,q). Dengan demikian, garis tersebut merupakan sumbu simetri.
Persamaan sumbu simetri untuk grafik fungsi di samping adalah x = p.

Tentukan persamaan sumbu simetri grafik y = f(x)= x2 + 2x – 3

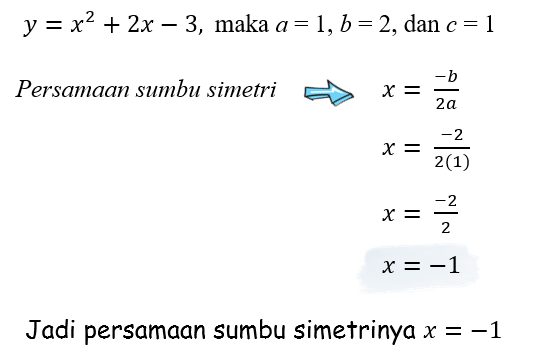

Rumus titik balik minimum/maksimum :
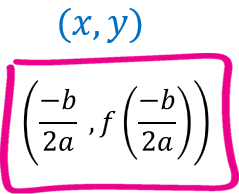


Tentukan titik balik minimum/maksimum untuk persamaan y = f(x)= x2 + 2x – 3



Jadi titik balik MINIMUM (karena a positif) adalah (–1, –4)
Nilai mimimumnya –4

Contoh Soal
CONTOH 1
Gambar berikut merupakan grafik fungsi y = f(x)= 5 + 4x – x2



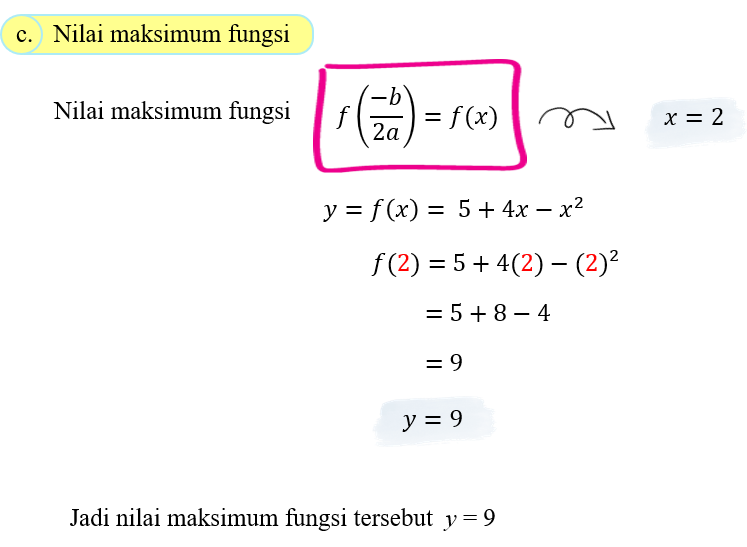




CONTOH 2
Gambar berikut merupakan grafik fungsi y = f(x)= x2 – 16




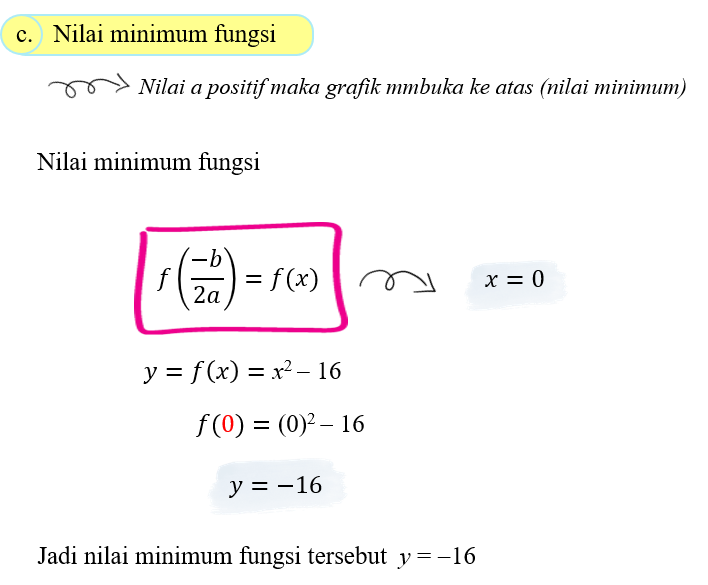



Jika dilihat dari gambar, posisi titik L ada di sebelah kiri, artinya
x = q = bernilai negatif. Maka q = –5
Penjelasan materi di atas bisa kalian saksikan pada video berikut ini.
Selamat belajar…


SOAL 1
Sebuah fungsi dinyatakan dengan rumus y = f(x) = x² − 6x −16, x ∊ R. Tentukan :
- Titik potong grafik dengan sumbu x
- Titik potong grafik dengan sumbu y
- Persamaan sumbu simetri grafik
- Nilai minimum fungsi
- Koordinat titik balik minimum
- Gambar grafik
SOAL 2
Sebuah fungsi dinyatakan dengan rumus y = f(x) = 6 + x – x2 dengan daerah asal -3 < x < 4, x ∊ R. Tentukan :
- Pembuat nol fungsi
- Titik potong grafik dengan sumbu y
- Nilai maksimum fungsi dan koordinat titik balik maksimum
- Daerah hasil fungsi
- Gambar grafik
SOAL 3
Sebuah fungsi dinyatakan dengan rumus y = f(x) = x² − 2x − 8, x ∊ R. Tentukan :
- Pembuat nol fungsi
- Titik potong grafik dengan sumbu y
- Nilai minimum fungsi
- koordinat titik balik minimum
- Gambar grafik
SOAL 4
Sebuah fungsi dinyatakan dengan rumus y = f(x) = x² + x − 12, x ∊ R. Tentukan:
- Pembuat nol fungsi
- Titik potong dengan sumbu y
- Nilai minimum fungsi
- Nilai m, jika C(−5, m) terletak pada grafik
- Nilai n, dimana D(n, −6) terletak pada grafik