Pernahkah kalian memperhatikan tulisan yang tertera pada kemasan obat?

—> Nah kalau diperhatikan, apa arti 3 x 1?
Artinya 1 diminum pagi hari, satu diminum siang hari, dan 1 diminum malam hari.

Jadi 3 x 1 = 1 + 1 + 1
💠 Nah, apa bedanya 3 x 4 dengan 4 x 3 ?
3 x 4 = … + … + …
4 x 3 = … + … + … + …
💠 Perkalian Bilangan Bulat Positif dan negatif
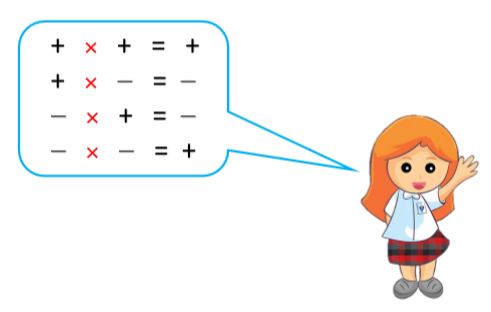
Sifat-Sifat Perkalian Bilangan Bulat
1. Sifat Komutatif (Pertukaran)
Untuk Setiap bilangan bulat a dan b, akan selalu berlaku ketentuan a x b = b x a.
Contoh :
a) 2 x 10 = 10 x 2
b) 12 x (-3) = (-3) x 12
2. Sifat Asosiatif (Pengelompokan)
Untuk Setiap bilangan bulat baik a, b, maupun c akan selalu berlaku ketentuan (a x b) x c = a x (b x c)
Contoh :
a) (2 x 6) x 7 = 84 dan 2 x (6 x 7) = 84
b) ((–3) x (–15)) x 2 = 90 dan (–3) x ((–15) x 2) = 90
3. Mempunyai Unsur Identitas
Bilangan 1 ( satu ) pada perkalian merupakan unsur identitas. Untuk Sembarang bilangan bulat a, akan selalu berlaku ketentuan a x 1 = 1 x a = a.
Contoh :
1 x 15 = 15 dan 15 x 1 = 15
4. Sifat Distributif Perkalian
Perhatikan tabel berikut dan lengkapilah!
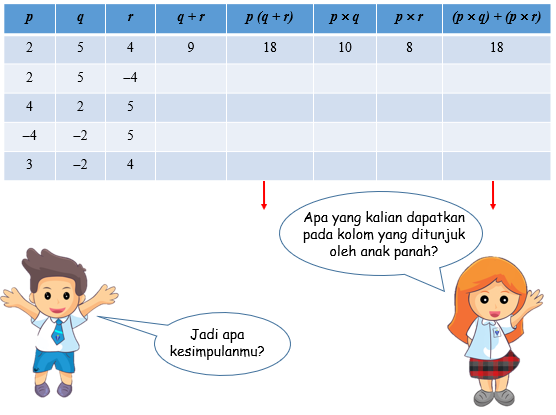
Contoh
Tentukan hasil perkalian bilangan-bilangan berikut!
a. –6 x 7
b. –5 x 2 x (–4)
c. –5 x ( 2 x (–9))
d. (–2 x 3) x [5 – (–3)]
e. [20 + (–15)] x (–5)
f. [15 + (– 4)] x [–5 – (–13)]

a. –6 x 7 = –42
b. –5 x 2 x (–4) = 40
c. –5 x ( 2 x (–9)) = –5 x ( –18) = 90
d. (–2 x 3) x [5 – (–3)] = (–6) x [5 + 3)] = –6 x 8 = –48
e. [20 + (–15)] x (–5) = 5 x (–5) = –25
f. [15 + (– 4)] x [–5 – (–13)] = 11 x (–5 +13) = 11 x 8 = 88
Penjelasan materi di atas bisa kalian saksikan pada video berikut ini.
Selamat belajar…
Latihan
SOAL 1
Hitunglah perkalian bilangan-bilangan berikut ini!
a. 12 x (–11) x (–15)
b. 9 x (–3) x (–6)
c. (–21) x (–30)
d. (–15) x 0 x (–18)
e. (–3) x (–6) x (–2) x (–1)
SOAL 2
Tentukan nilai n sehingga pernyataan-pernyataan di bawah ini menjadi kalimat yang benar
a. n x (–7) = 63
b. n x –8 = –64
c. –25 x 3 x n = –150
d. –2 x n x (–6) = –108
SOAL 3
Hitunglah nilai operasi bilangan-bilangan berikut ini (gunakan cara yang paling mudah)!
a. 24 x (–45) + (–45) x (–34)
b. 8 x 53 x (–125)
c. 15 x (–25) x (–4) x (–10)
d. 6 x (100 – 2)
e. (–57) x (–19) + 57
f. (15 x 6) – 7 – (–2 x 18)
SOAL 4
Suhu mula-mula adalah 30°C dan akan turun 3°C setiap jam. Berapakah suhu setelah 10 jam?
SOAL 5
Dalam ulangan matematika yang terdiri dari 40 soal, ditentukan aturan sbb: jika dapat menjawab benar mendapat skor 4, jika menjawab salah mendapat skor –2, dan jika tidak menjawab mendapat skor –1. Ternyata Agus dapat menjawab benar sebanyak 22 soal dan menjawab salah sebanyak 3 soal, berapa skor yang diperoleh oleh Agus?
SOAL 6
Suhu pada jam 12 siang adalah 10°C di atas nol. Jika berkurang 2°C setiap jam hingga tengah malam,
a. pada jam berapakah suhunya menjadi 8°C di bawah nol?
b. berapakah suhu pada tengah malam (pukul 00.00)?
SOAL 7
Sebuah perusahaan mendapatkan untung Rp 800 per kantong semen putih yang terjual dan kerugian Rp500,00 per kantong semen abu-abu yang terjual.
a.Jika perusahaan menjual 3.000 kantong semen puih dan 5.000 kantong semen abu-abu dalam sebulan. Untung atau rugikah perusahaan tersebut?
b.Jika perusahaan itu menjual 6.400 kantong semen abu-abu, berapa paling sedikit kantong semen putih yang harus di jual supaya perusahaan tersebut tidak rugi?